17. Scipy Tutorial- 非整周期信号加窗
17.1 什么是加窗？
使用FFT分析信号的频率成分时，分析的是有限的数据集合。 FFT认为波形是一组有限数据的集合，一个连续的波形是由若干段小波形组成的。 对于FFT而言，时域和频域都是环形的拓扑结构。时间上，波形的前后两个端点是相连的。 如测量的信号是周期信号，采集时间内刚好有整数个周期，那么FFT的上述假设合理。
下面以采样率200$Hz$为例来解释一下以上的论述，采样率200$Hz$即$f_s = 200Hz$，每秒采集200个点数据。在看测试的信号，正弦波$f = sin(10 * 2\pi t)$，那么该正弦波的频率为$10Hz$，周期为0.1s，那么1s采集数据可以得到10个正弦波的数据，每个正弦波有20条数据。1s采集的数据用于fft分析可以得到正确的分析结果。
#coding:utf-8
import numpy as np
import pylab as pl
from scipy import fftpack,signal
import matplotlib.pyplot as plt
sampling_rate = 100
f_s = 2 * sampling_rate
T = 1
t = np.linspace(0, T, f_s)
x = np.sin(2 * np.pi * 10 * t)
F = fftpack.fft(x)
f = fftpack.fftfreq(T * f_s, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(2, 1, figsize=(8, 6))
axes[0].plot(t, x, label="Oringal")
axes[0].set_xlabel("times (s)", fontsize=14)
axes[1].plot(f[mask], abs(F[mask])/(f_s*T), label="Frequency")
axes[1].set_xlabel("frequency (Hz)", fontsize=14)
plt.show()
执行结果：
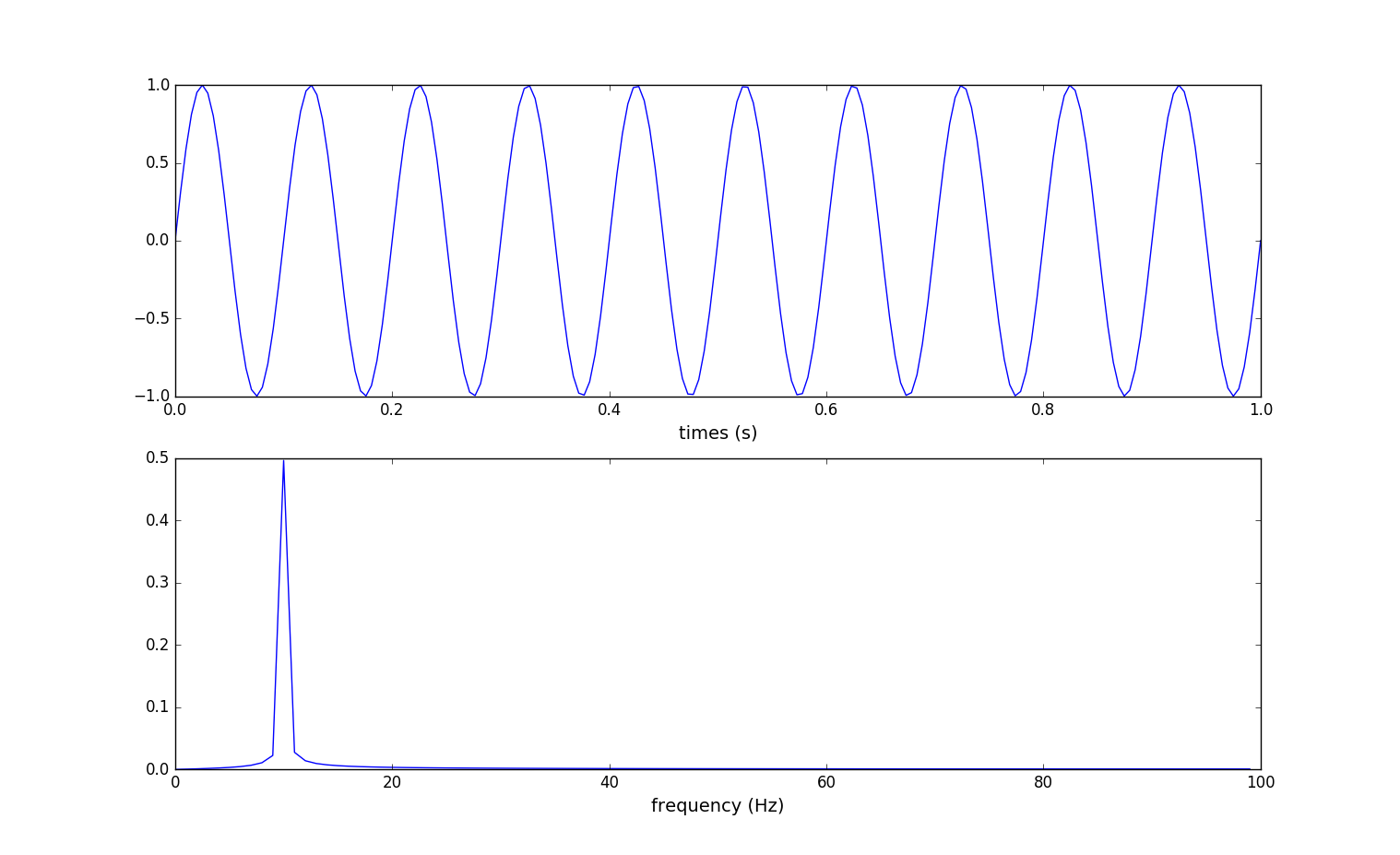这里采样1s获得了10个$f = sin(10 * 2\pi t)$正弦波完整数据来进行fft分析，结果很完美。
- 采集到的周期信号完整性和个数对fft的影响
问题来了，如果用1个、2个、3个$f = sin(10 * 2\pi t)$正弦波去进行fft分析会得到如此完美的结果么？半个$f = sin(10 * 2\pi t)$正弦波可以么？
#coding:utf-8
import numpy as np
import pylab as pl
from scipy import fftpack,signal
import matplotlib.pyplot as plt
sampling_rate = 100
f_s = 2 * sampling_rate
T = np.arange(1,21) * 0.05
def drawT(T):
print "t", T
t = np.linspace(0, T, T * f_s)
x = np.sin(2 * np.pi * 10 * t)
F = fftpack.fft(x)
f = fftpack.fftfreq(int(T * f_s), 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(2, 1, figsize=(8, 6))
axes[0].plot(t, x, label="Oringal")
axes[0].set_xlabel("times (s)", fontsize=14)
axes[1].plot(f[mask], abs(F[mask])/(f_s*T), label="Frequency")
axes[1].set_xlabel("frequency (Hz)", fontsize=14)
plt.show()
for ti in T:
drawT(ti)
print "end"
(1).这个采集了0.05s得到半个$f = sin(10 * 2\pi t)$正弦波得到的结果图：
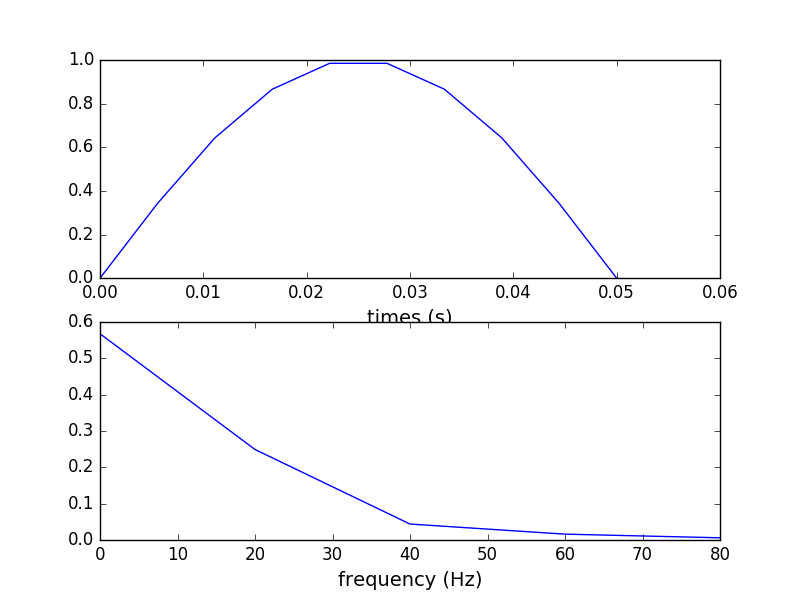这个结果基本看不出啥内容，频率很不好！
(2).采集0.1s得到一个完整的$f = sin(10 * 2\pi t)$正弦波进行fft分析的结果：
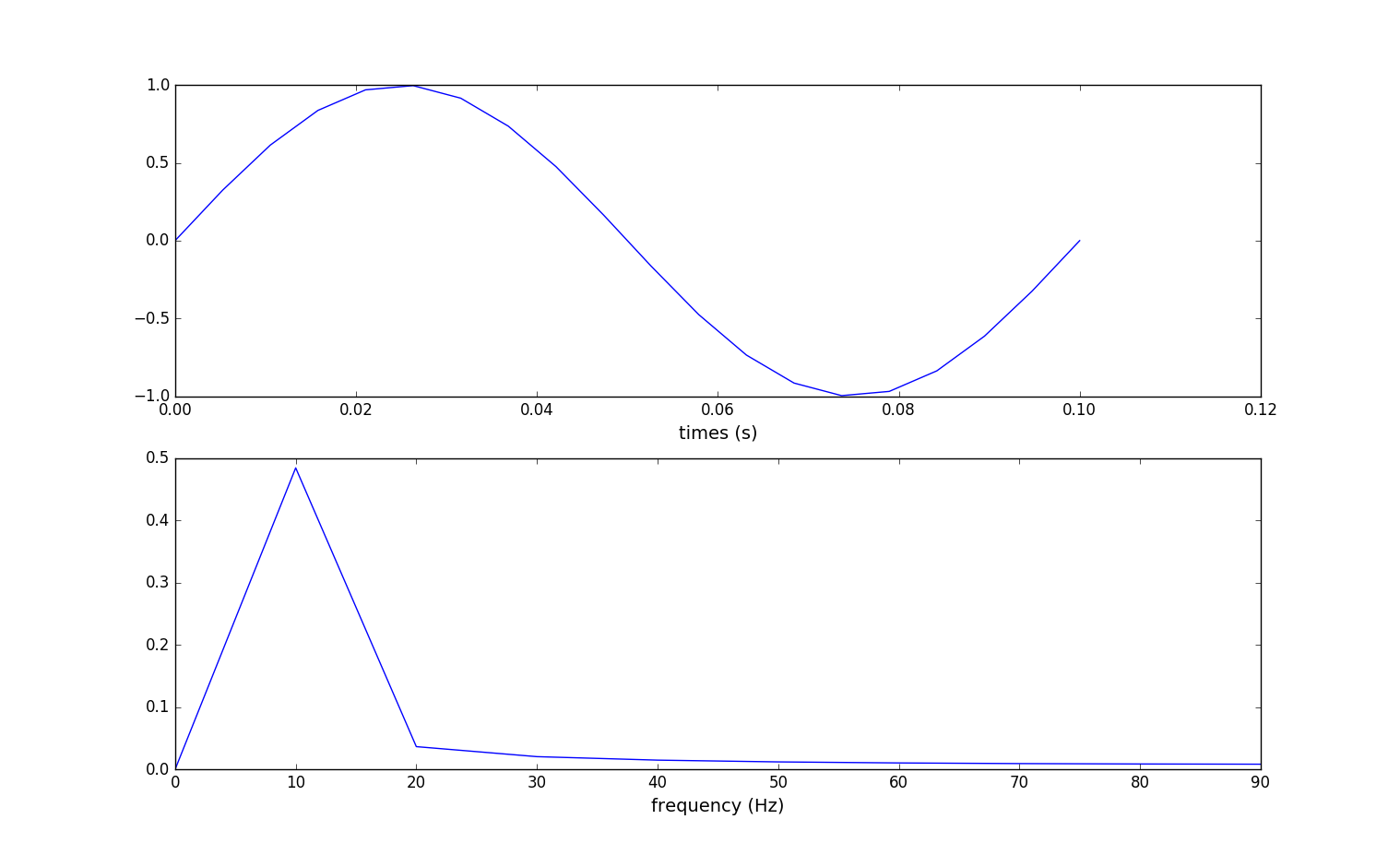结果好点儿。能看出频峰出现在$10Hz$的意思了。
(3).采集0.15s可以得到1个半的正弦波，结果：
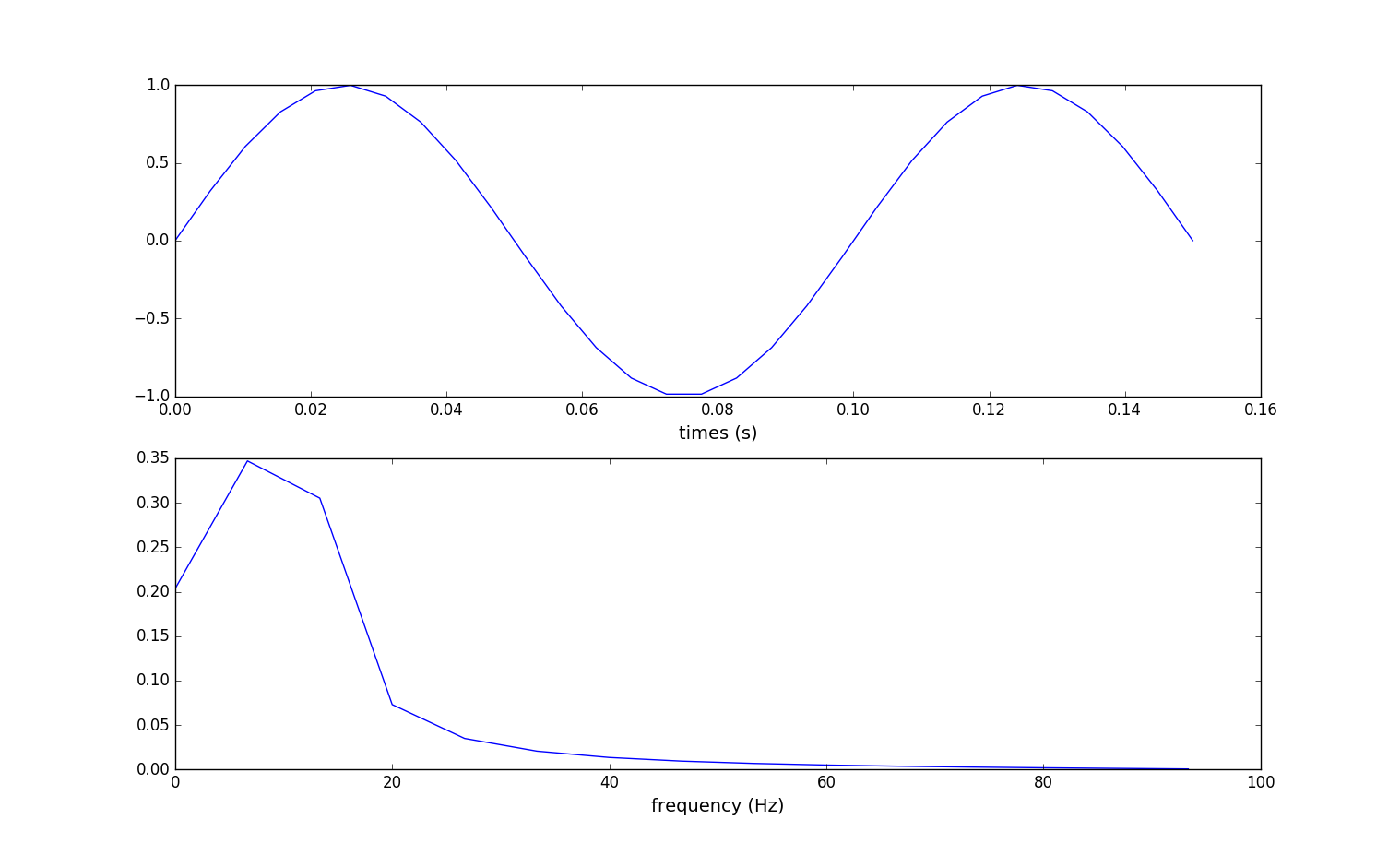结果不完美
(4).采集0.2s得到两个完整正弦波，进行fft处理后的结果图：
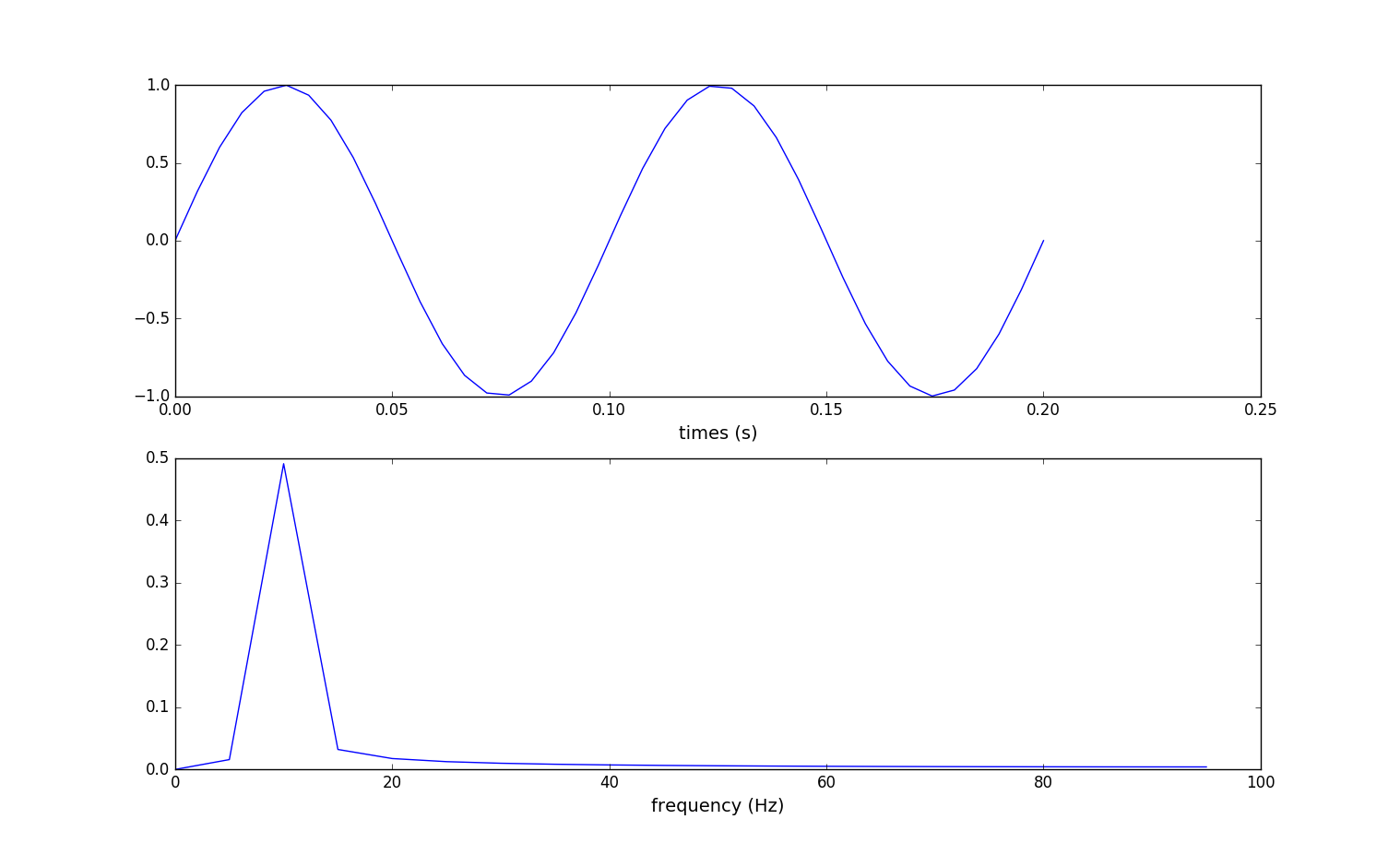结果比01.s的更加完美。
(5).采集0.4s得到四个完整正弦波，进行fft处理后的结果图：
结果比02.s的更加完美，频峰出现在$10Hz$很明显。
(6).采集了0.45s的四个半正弦波，结果又不完美了。
随着程序的不断执行。
(7).采集了1s的数据共10个完整的正弦波，经fft处理：
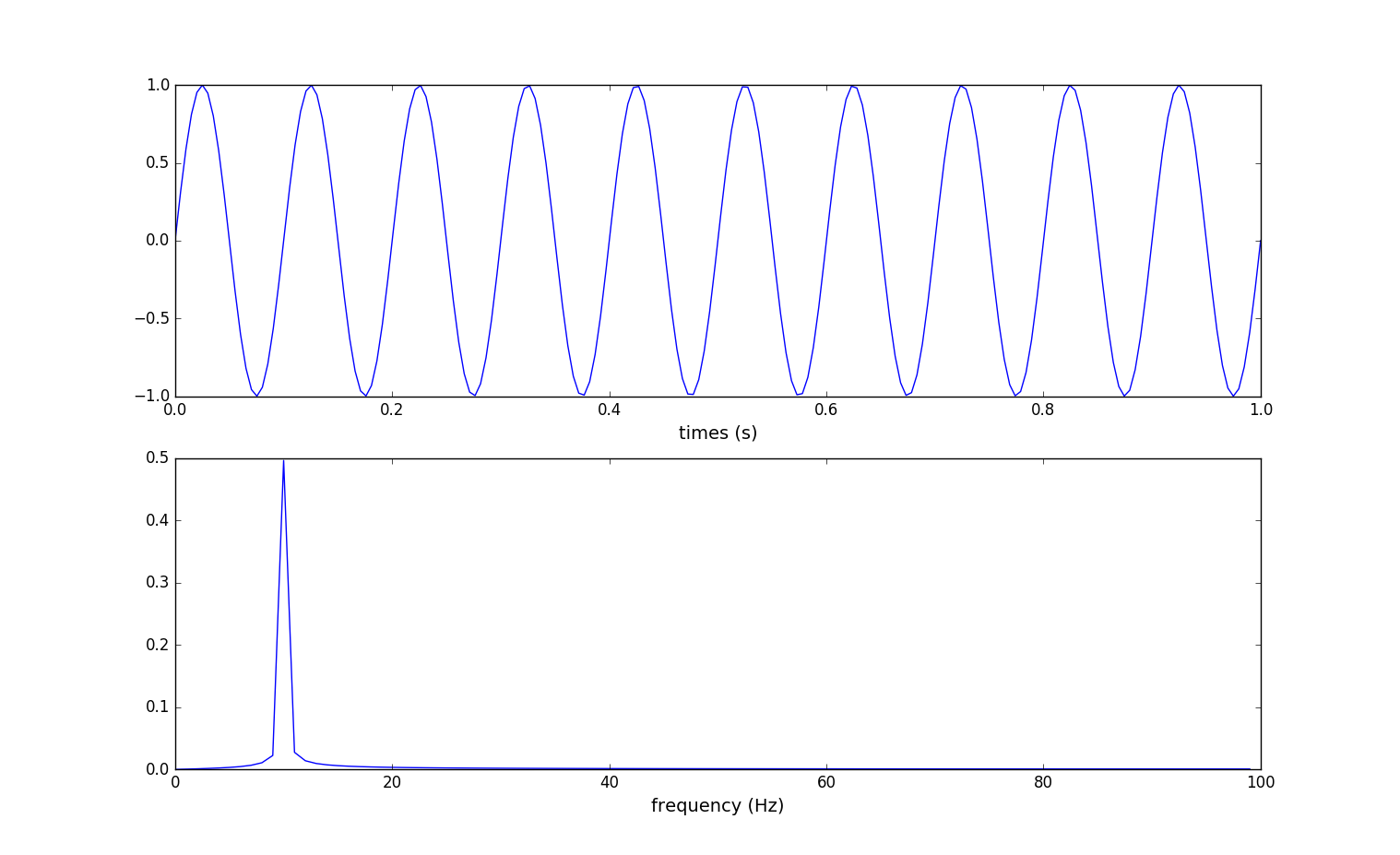结果比之前的都完美，频峰出现在$10Hz$非常明显。
结论：从这个程序可以看出，完整采集了正弦波后fft的处理结果比较完美，而不完整的正弦波的fft结果有些瑕疵，另外完整波个数越多结果越完美。
- 不完整的周期信号对fft的影响
在有限的时间段中对信号进行测量，无法知道在测量范围之外的信号是怎样的。因此只能对测量范围之外的信号进行假设。而傅立叶变换的假设很简单：测量范围之外的信号是所测量到的信号的重复。
在很多情况下，并不能测量到整数个周期，然后把这个非完整周期数据重复n次，再用fft分析。那么由于数据是从信号周期中间切断获得的，与时间连续的原信号显示出不同的特征。有限数据采样会使测量信号产生剧烈的变化。 这种剧烈的变化称为不连续性。采集到的周期为非整数时，端点是不连续的。 这些不连续片段在FFT中显示为高频成分。这些高频成分不存在于原信号中。 (1). 首先看看例子在能采集出完整周期信号波的fft分析。
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
sampling_rate = 1000
f_s = 2 * sampling_rate
N = 80
T = 1
t = np.linspace(0, T, f_s)[:N]
x = np.sin(2 * np.pi * 50 * t)[:N]
t10 = np.linspace(0, 10 * T * N * 1.0 / f_s, 10 * f_s * N * 1.0 / f_s)
x10 = np.tile(x, 10)
F = fftpack.fft(x10)
f = fftpack.fftfreq(10 * N, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(3,1)
axes[0].plot(t, x)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("signal")
axes[1].plot(t10, x10)
axes[1].set_xlabel("time (s)")
axes[1].set_ylabel("signal")
axes[2].plot(f[mask], abs(F[mask])/N, label="real")
axes[2].set_xlabel("Frequency (Hz)")
axes[2].set_ylabel("F")
plt.show()
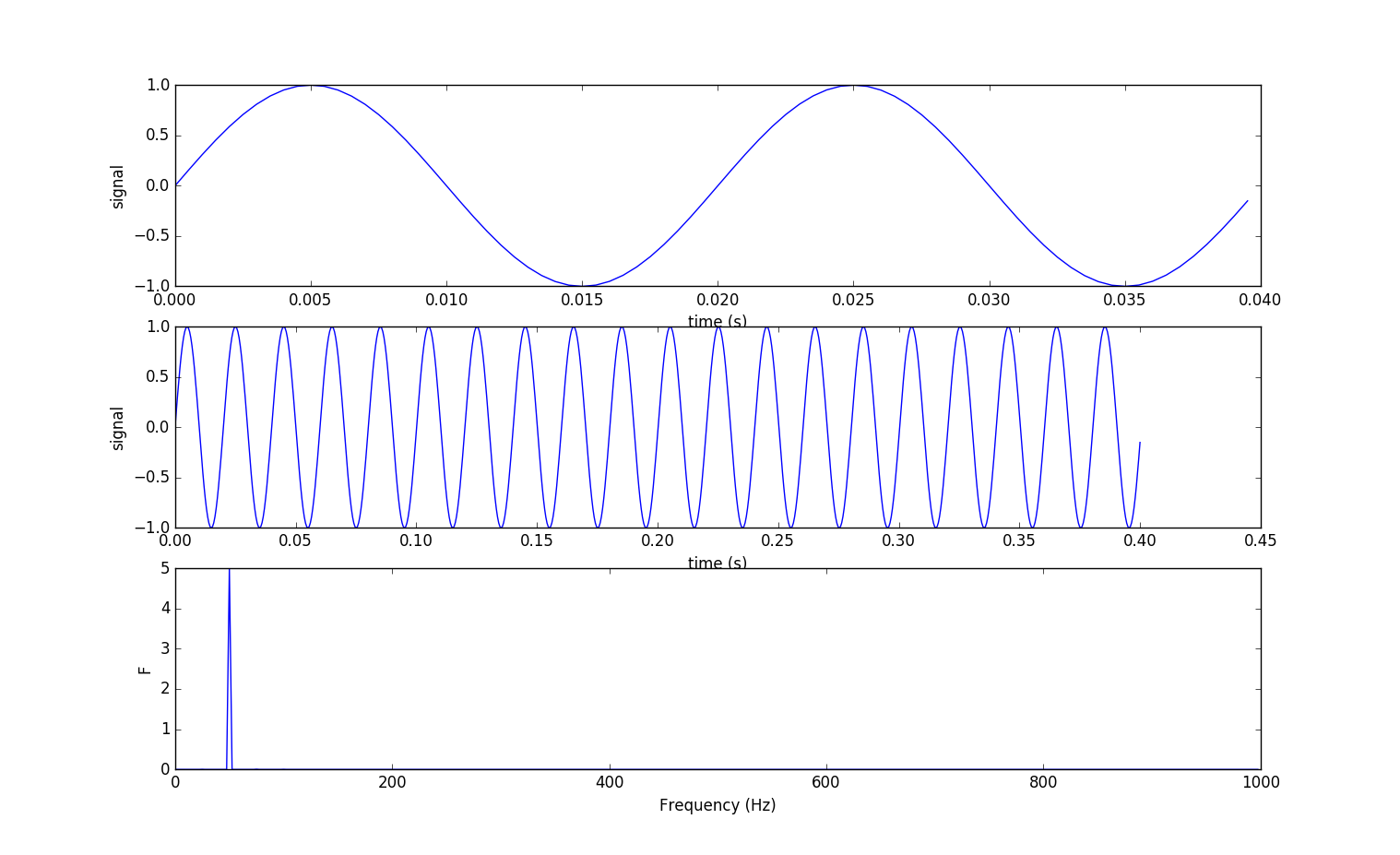上图最下的子图，比较完美，就一个频峰，大致$50Hz$处出现的。
为何？采样率2000Hz，1s采集2000条数据，正弦波的频率是50Hz那么1s会有50个正弦波，每个正弦波有40条数据，那么80条数据(语句x = np.sin(2 * np.pi * 50 * t)[:N])即$N = 80$会采样得到几个正弦波呢？
$$
n = \frac{80}{\frac{2000}{50}} = \frac{80}{40} = 2
$$
得到2个完整的正弦波，即子图1。将80个数据的2个正弦波重复10次(语句x10 = np.tile(x, 10))得到子图2，便可进行fft处理了，得到子图3。.
(2).非完整周期信号，程序里只需将N由80改为55个数据点。
#coding:utf-8
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
sampling_rate = 1000
f_s = 2 * sampling_rate
N = 55
T = 1
t = np.linspace(0, T, f_s)[:N]
x = np.sin(2 * np.pi * 50 * t)[:N]
t10 = np.linspace(0, 10 * T * N * 1.0 / f_s, 10 * f_s * N * 1.0 / f_s)
x10 = np.tile(x, 10)
F = fftpack.fft(x10)
f = fftpack.fftfreq(10 * N, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(3,1)
axes[0].plot(t, x)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("signal")
axes[1].plot(t10, x10)
axes[1].set_xlabel("time (s)")
axes[1].set_ylabel("signal")
axes[2].plot(f[mask], abs(F[mask])/N, label="real")
axes[2].set_xlabel("Frequency (Hz)")
axes[2].set_ylabel("F")
plt.show()
这个结果很意外么？对比此图的2、3子图和上一个图的2、3子图，在本图的2子图是非连续的信号(大致在0.025s$\sim$0.3s间)，所以在本图的3子图里出现了很多的频峰，能量被分散到其他频率里去了。之后使用FFT获得的频率，不是原信号的实际频率，而是一个改变过的频率。 类似于某个频率的能量泄漏至其他频率，这种现象叫做频谱泄漏。频率泄漏使好的频谱线扩散到更宽的信号范围中。谱泄漏对频谱图的影响的大小取决于时域图中边界上的不连续程度。加窗方法可以将这种不连续最小化。窗函数实质上是一个加权函数。通过加窗函数与原始函数相乘，改善能量泄露的状况。
程序里$N = 55$只是截取了
$$
n = \frac{55}{\frac{2000}{50}} = \frac{55}{40} = 1 \frac{3}{8}
$$
个正弦波(语句x = np.sin(2 * np.pi * 50 * t)[:N])，见子图1。重复10次(见语句x10 = np.tile(x, 10))，见子图2。fft分析里有很多频率来源于子图2里的不连续点(大致在0.025s$\sim$0.3s间)。如何解决？阅读下一节。
17.2 加窗函数
可通过加窗来尽可能减少在非整数个周期上进行FFT产生的误差。 数字化仪采集到的有限序列的边界会呈现不连续性。加窗可减少这些不连续部分的幅值。 加窗包括将时间记录乘以有限长度的窗，窗的幅值逐渐变小，在边沿处为0。 加窗的结果是尽可能呈现出一个连续的波形，减少剧烈的变化。 这种方法也叫应用一个加窗。
根据信号的不同，可选择不同类型的加窗函数。 要理解窗对信号频率产生怎样的影响，就要先理解窗的频率特性。
窗的波形图显示了窗本身为一个连续的频谱，有一个主瓣，若干旁瓣。 主瓣是时域信号频率成分的中央，旁瓣接近于0。 旁瓣的高度显示了加窗函数对于主瓣周围频率的影响。 对强正弦信号的旁瓣响应可能会超过对较近的弱正弦信号主瓣响应。 一般而言，低旁瓣会减少FFT的泄漏，但是增加主瓣的带宽。 旁瓣的跌落速率是旁瓣峰值的渐进衰减速率。 增加旁瓣的跌落速率，可减少频谱泄漏。
选择加窗函数并非易事。 每一种加窗函数都有其特征和适用范围。 要选择加窗函数，必须先估计信号的频率成分。加窗规则：
(1).如果您的信号具有强干扰频率分量，与感兴趣分量相距较远，那么就应选择具有高旁瓣下降率的平滑窗。 (2).如果您的信号具有强干扰频率分量，与感兴趣分量相距较近，那么就应选择具有低最大旁瓣的窗。 (3).如果感兴趣频率包含两种或多种很距离很近的信号，这时频谱分辨率就非常重要。 在这种情况下，最好选用具有窄主瓣的平滑窗。 (4).如果一个频率成分的幅值精度比信号成分在某个频率区间内精确位置更重要，选择宽主瓣的窗。 (5).如信号频谱较平或频率成分较宽，使用统一窗，或不使用窗。 总之，Hanning窗适用于95%的情况。 它不仅具有较好的频率分辨率，还可减少频谱泄露。 如果您不知道信号特征但是又想使用平滑窗，那么就选择Hanning窗。
即使不使用任何窗，信号也会与高度一致的长方形窗进行卷积运算。本质上相当于对时域输入信号进行截屏，对离散信号也有效。 该卷积有一个正弦波函数特性的频谱。 基于该原因，没有窗叫做统一窗或长方形窗。
Hamming窗和Hanning窗都有正弦波的外形。 两个窗都会产生宽波峰低旁瓣的结果。 Hanning窗在窗口的两端都为0，杜绝了所有不连续性。 Hamming窗的窗口两端不为0，信号中仍然会呈现不连续性。 Hamming窗擅长减少最近的旁瓣，但是不擅长减少其他旁瓣。 Hamming窗和Hanning适用于对频率精度要求较高对旁瓣要求较低的噪声测量。
如果截断的信号仍为周期信号，则不存在泄漏，无须加窗，相当于加矩形窗。
下面以频率为50$Hz$的正弦波为例，采样率2000$Hz$那么每秒有50个正弦波，每秒采样2000个点儿数据，每个正弦波占40条数据。为了模拟实际测量时非周期截断信号，这里提取55个数据点儿，即不到一个半的正弦波做为工作中实际测量截断的数据。如下图子图1。
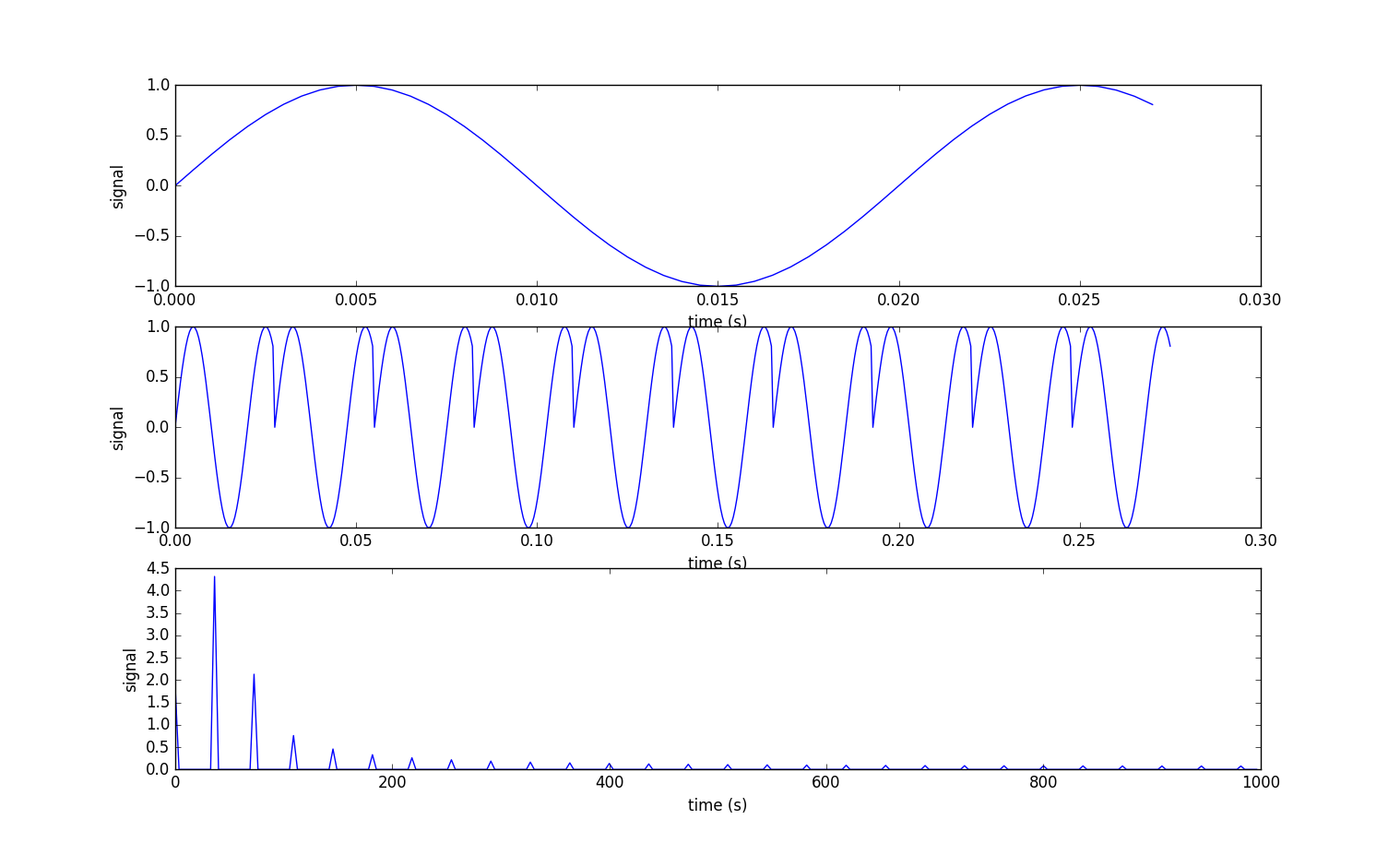为了做fft频谱分析，需要尽量多点儿数据，所以对这55个数据的信号(x)进行了重复之后(周期性延拓)，再传给fft去分析频率，所以这里重复10次x信号(x10)得到上图的子图2。子图2里有不连续的尖点(例如：0.025s$\sim$0.3s间)，尖点附近频率跳动频繁，而且多是高频信号，所以这样的信号如果直接被fft处理，那么频率分布范围较广，如上图子图3所示。回到本节开始可以考虑给信号加窗，改变尖点处的不连续情况，尽量让信号曲线平滑一些即连续从而减少频谱泄漏的现象。
#coding:utf-8
import numpy as np
from scipy import fftpack,signal
import matplotlib.pyplot as plt
sampling_rate = 1000
f_s = 2 * sampling_rate
N = 55
T = 1
t = np.linspace(0, T, f_s)[:N]
x = np.sin(2 * np.pi * 50 * t)[:N]
t10 = np.linspace(0, 10 * T * N * 1.0 / f_s, 10 * f_s * N * 1.0 / f_s)
x10 = np.tile(x, 10)
F = fftpack.fft(x10)
f = fftpack.fftfreq(10 * N, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(3,1)
axes[0].plot(t, x)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("signal")
axes[1].plot(t10, x10)
axes[1].set_xlabel("time (s)")
axes[1].set_ylabel("signal")
axes[2].plot(f[mask], abs(F[mask])/N, label="real")
axes[2].set_xlabel("time (s)")
axes[2].set_ylabel("signal")
plt.show()
from scipy import fftpack,signal
window = signal.hann(len(x), sym = 0) * 2
x10w = np.tile(x * window, 10)
F_w = fftpack.fft(x10w)
F = fftpack.fft(x10)
f = fftpack.fftfreq(10 * N, 1.0/f_s)
mask = np.where(f >= 0)
fig, axes = plt.subplots(4, 1, figsize=(8, 6))
axes[0].plot(t10, x10)
axes[0].set_xlabel("time (s)")
axes[0].set_ylabel("Signal")
axes[1].plot(t10, x10w, label="real")
axes[1].set_ylabel("$Signal_w$")
axes[2].plot(f[mask], abs(F[mask])/f_s, label="real")
axes[2].set_ylabel("$|F|$", fontsize=14)
axes[3].plot(f[mask], abs(F_w[mask])/f_s, label="real")
axes[3].set_xlabel("frequency (Hz)", fontsize=14)
axes[3].set_ylabel("$|F_w|$", fontsize=14)
plt.show()
现在分析一下这个程序，程序设定的采样率为2000$Hz$即每秒采集信号2000个点数据，用f_s表示。程序里的正弦波的频率为$50Hz$,其意义是每秒有50个这样的正弦波出现或者产生，那么每40个数据就是一个频率为$50Hz$的正弦波。为了演示截断造成的频谱泄漏设定截断信号个数N为55，那么55个数据可以表示：
$$
n = \frac{55}{\frac{2000}{50}} = \frac{55}{40} = 1 \frac{3}{8}
$$
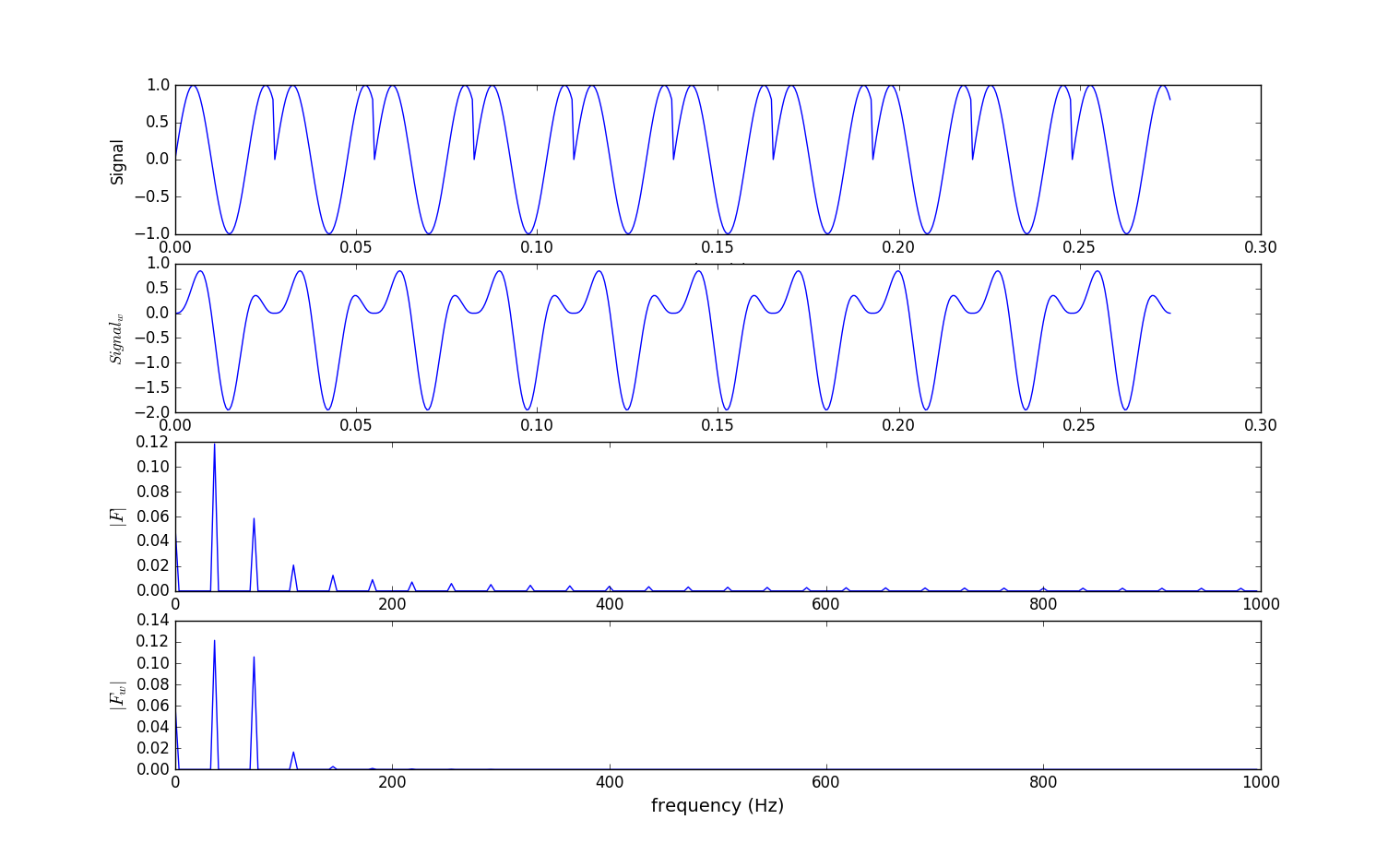
个正弦波(语句x = np.sin(2 * np.pi * 50 * t)[:N])。为了提高分析准确度需尽量给fft传入周期性数据，那么将N为55的截断非完整周期长度的“正弦波”重复(周期性延拓)10次(见语句x10 = np.tile(x, 10))，这样传入fft的数据量就比较可观了。当然采集时间也得同步增长10倍t10 = np.linspace(0, 10 * T * N * 1.0 / f_s, 10 * f_s * N * 1.0 / f_s)。这时将x10传给fft去处理得到$F$，这个频谱是未经加窗处理的频谱，其频率特性可以参看下图子图3,在$0\sim 1000Hz$这个频率范围内均有频峰出现，显然是下图子图1里的尖点的不连续而造成的，那么希望对这些尖点进行平滑连续，可以对下图子图1的采集信号进行加窗处理变成下图子图2的样子。
window = signal.hann(len(x), sym = 0) * 2 #信号加窗
x10w = np.tile(x * window, 10) #10倍扩展重复
注意这加窗是对截断的55点的信号$x$进行加窗而不是x信号的10倍信号$x10$加窗，这样，扩展10倍后得到$x10w$,然后将$x10w$传给fft函数去分析频率得到$F_w$。程序里为了展示加窗和未加窗的对比效果还对未加窗信号$x10$也进行了fft处理得到$F$。
F_w = fftpack.fft(x10w)
F = fftpack.fft(x10)
从下图的子图3(未加窗)和子图4(加窗)可以看出未加窗的信号$x10$的频谱$F$在$200Hz\sim1000Hz$有频峰出现，而加窗了的信号$x10w$的频谱$F_w$在$200Hz\sim1000Hz$几乎有频峰出现，频率更加集中在$0Hz\sim 200Hz$这个范围内。更接近50$Hz$正弦信号的频率值。
17.3 总结
实际测量工作中尽量截断整周期的信号来进行fft分析;加窗可以使截断两端更平滑，截断时间如果可能尽量长。