16. SciPy二元样条插值

之前的章节的插值基本上都是一个变量x，本章就二元(二维)的插值问题进行展开。 在SciPy模块库的scipy.interpolate子模块里提供了interp2d方法函数可以实现二维插值。

16.1 绘制二元可视化数据

Python里可视化输出的模块很多，但比较常用的是matplotlib模块来实现数据的可视化的输出。在matplotlib模块里的子模块pyplot里提供很多的类似matlib的一些绘制函数，本章、本网并没有意愿详述matplotlib模块库，有意学习pyplot的可以访问其官方网站系统学习。 1). 用matplotlib绘制二维可视化数据首先要引入相应的模块库。

import numpy as np, matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D

这里还引入了mpl_toolkits.mplot3d.axes3d模块，目前是支持三维显示。

2). 接下来可以定义一个二元的$f(x, y)$函数。

def f(x,y):
    return np.sin(x) + np.sin(y)

3). 定义网格数据：

t = np.linspace(-3, 3, 100)
domain = np.meshgrid(t, t)

有关meshgrid函数可以参考本站的NumPy部分的meshgird函数内容。domain变量是一个列表，里面有两个numpy的array。再将网格数据提取出来作为X和Y。在将X和Y代入$f(x, y)$函数得到Z值。

X, Y = domain
Z = f(*domain)

4). 绘制$f(x, y)$，这里使用了subplot2grid函数。

fig = plt.figure()
ax1 = plt.subplot2grid((2,2), (0,0), aspect='equal')
p = ax1.pcolor(X, Y, Z)
fig.colorbar(p)
CP = ax1.contour(X, Y, Z, colors='k')
ax1.clabel(CP)
ax1.set_title('Contour plot')

语句subplot2grid((2,2), (0,0), aspect='equal')的含义是整个绘制图是2行2列，此次绘制的ax1图像位于0行0列，而aspect参数传给内部调用的add_subplot函数使用,'equal'参数的含义可以查阅该函数。

语句 ax1.pcolor(X, Y, Z),这是在给此图配置颜色。

语句fig.colorbar(p)的colorbar函数的作用则是产生色度条。 语句CP = ax1.contour(X, Y, Z, colors='k')的contour函数绘制包络曲线。

语句ax1.clabel(CP)里的clalel函数的作用则是给绘制的包络曲线加注文字信息。 语句ax1.set_title('Contour plot')的set_title函数则是给子图添加一个标签名。

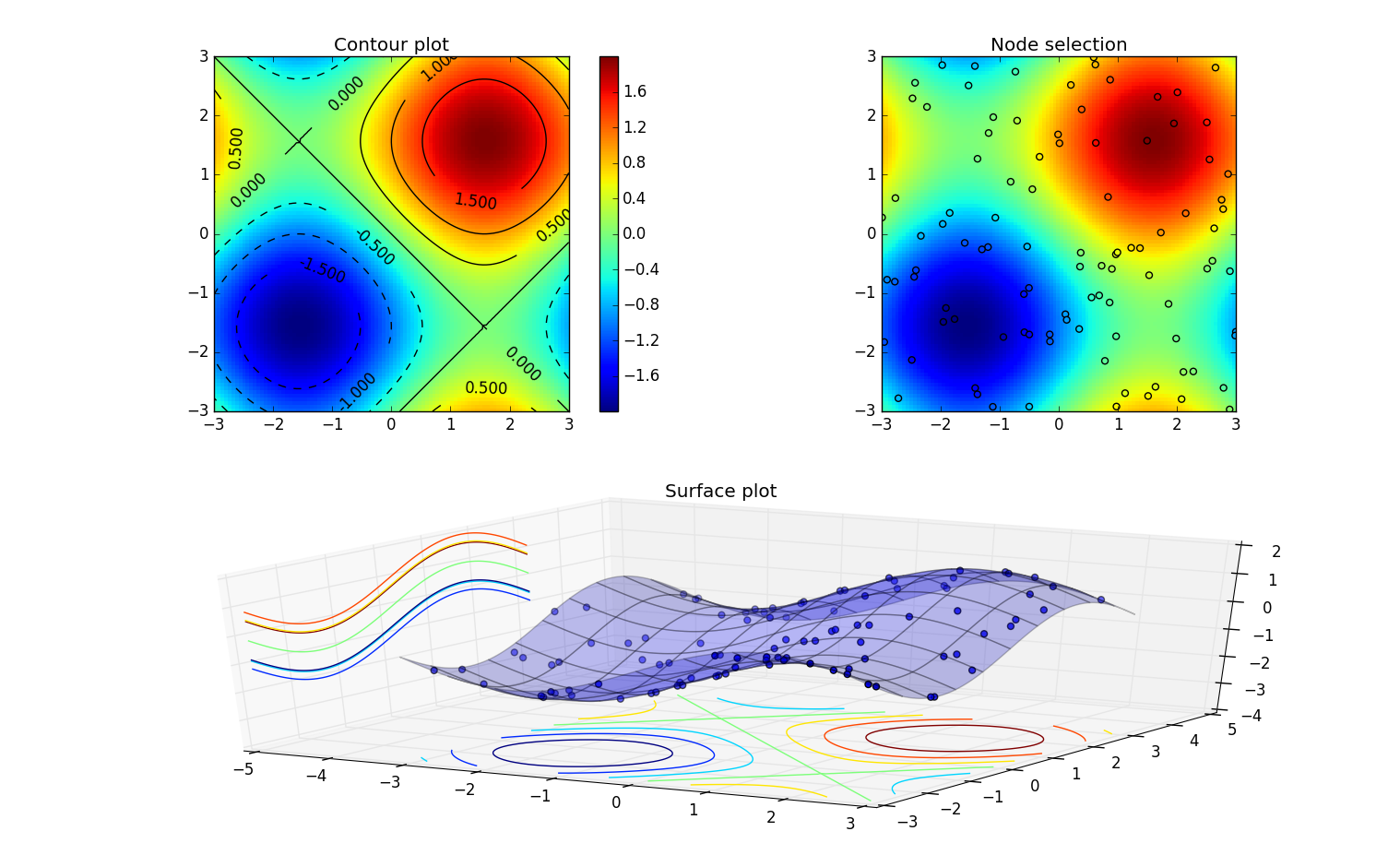
到此的代码的绘制的图像为下图里位置为左上的那个图。

16.2 绘制需要插值的点

1). 产生插值点

nodes = 6 * np.random.rand(100, 2) - 3
#print np.random.rand(100, 2)
xi = nodes[:, 0]
yi = nodes[:, 1]
zi = f(xi, yi)

NumPy的random模块下的rand函数可以产生$[0, 1)$区间的均匀分布，参数(100, 2)给出函数结构是一个100行2列的数组(ndarray)。第一列作为插值点的$x$，第二列作为$y$坐标。将$x$和$y$代入$f(x, y)$函数得到$z$值。

2). 绘制插值点的可视化图ax2

ax2 = plt.subplot2grid((2,2), (0,1), aspect='equal')
p2 = ax2.pcolor(X, Y, Z)
ax2.scatter(xi, yi, 25, zi)
ax2.set_xlim(-3, 3)
ax2.set_ylim(-3, 3)
ax2.set_title('Node selection')

这里用到了scatter函数，他的作用是绘制插值点nodes。set_xlim函数是设置显示图的范围。而其他函数在上一节里介绍过了。这部分代码被执行时会得到下图右上子图。 右上子图ax2小圆圈就是nodes的可视化结果。

16.3 二元3D可视化

这部分的内容是得到上图的下面的子图，即数据的3D可视化。

ax3 = plt.subplot2grid((2,2), (1,0), projection='3d', colspan=2, rowspan=2)
ax3.plot_surface(X, Y, Z, alpha=0.25)
ax3.scatter(xi, yi, zi, s=25)
cset = ax3.contour(X, Y, Z, zdir='z', offset=-4)
cset = ax3.contour(X, Y, Z, zdir='x', offset=-5)
ax3.set_xlim3d(-5, 3)
ax3.set_ylim3d(-3, 5)
ax3.set_zlim3d(-4, 2)
ax3.set_title('Surface plot')
fig.tight_layout()
plt.show()

subplot2grid里的projection='3d'形参的作用是说此图ax3是3D的。位置为(1, 0)由于后续没有(1, 1)位置的子图，那么此图ax3占整个第2行输出,绘制的X、Y、Z。 语句ax3.plot_surface(X, Y, Z, alpha=0.25)绘制的曲面。 而语句ax3.scatter(xi, yi, zi, s=25)则是3D绘制的nodes各个插值点。

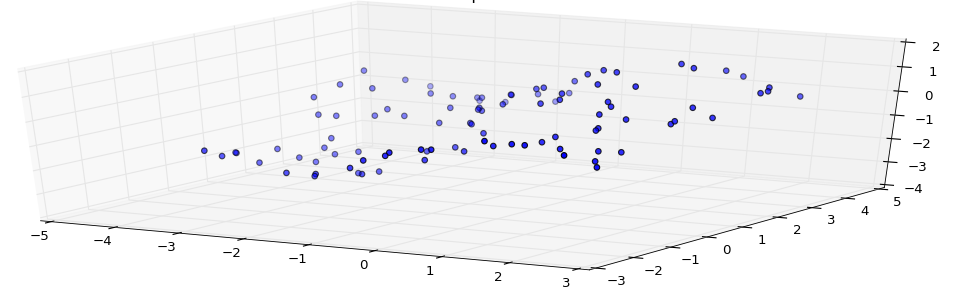
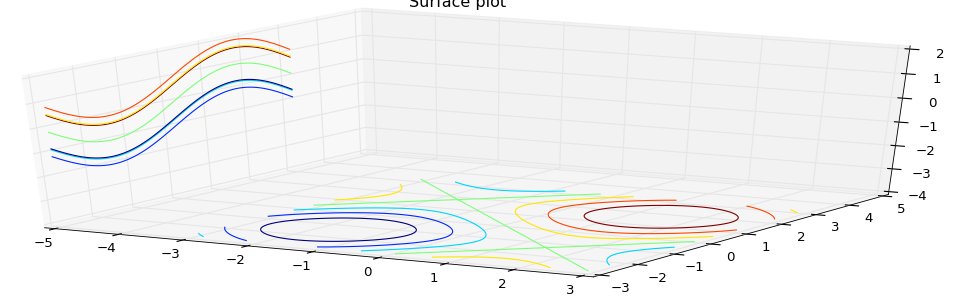
cset = ax3.contour(X, Y, Z, zdir='z', offset=-4)
cset = ax3.contour(X, Y, Z, zdir='x', offset=-5)

这两条语句则是绘制的X、Y、Z在xy平面、yz平面的投影曲线。

16.4 节点插值可视化

节点nodes准备好以后可以使用SciPy模块库的scipy.interpolate子模块里提供了interp2d方法函数对nodes进行线性插值。

from scipy.interpolate import interp2d
interpolant = interp2d(xi, yi, zi, kind='linear')

然后便可可视化输出。

plt.figure()
plt.axes().set_aspect('equal')
plt.pcolor(X, Y, interpolant(t, t))
plt.scatter(xi, yi, 25, zi)
CP = plt.contour(X, Y, interpolant(t, t), colors='k')
plt.clabel(CP)
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.title('Piecewise linear interpolation')
plt.show()

得到结果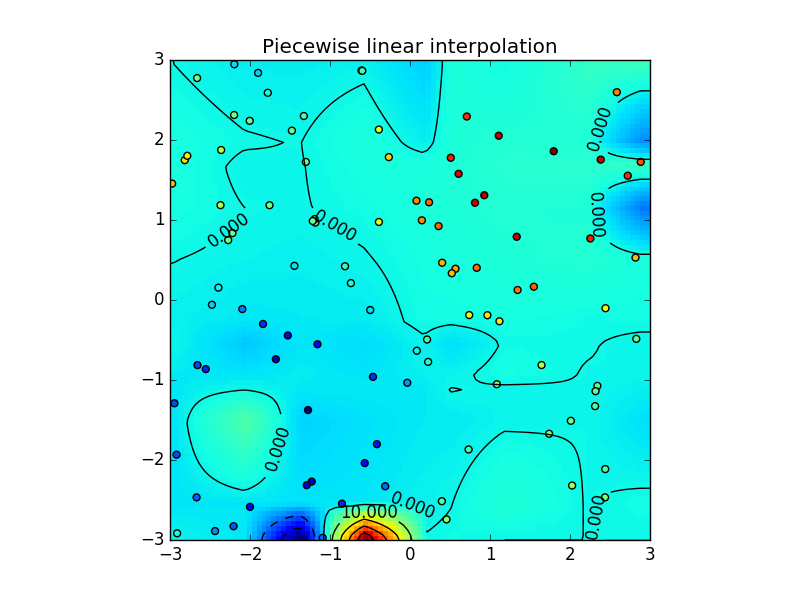： 需要注意的是nodes是随机产生的，每次运行程序的结果可能不一样。

16.5 完整的程序代码

import numpy as np, matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D

def f(x,y):
    return np.sin(x) + np.sin(y)

t = np.linspace(-3, 3, 100)
domain = np.meshgrid(t, t)
X, Y = domain
Z = f(*domain)

fig = plt.figure()
ax1 = plt.subplot2grid((2,2), (0,0), aspect='equal')
p = ax1.pcolor(X, Y, Z)
fig.colorbar(p)
CP = ax1.contour(X, Y, Z, colors='k')
ax1.clabel(CP)
ax1.set_title('Contour plot')

nodes = 6 * np.random.rand(100, 2) - 3
print np.random.rand(100, 2)
xi = nodes[:, 0]
yi = nodes[:, 1]
zi = f(xi, yi)

ax2 = plt.subplot2grid((2,2), (0,1), aspect='equal')
p2 = ax2.pcolor(X, Y, Z)
ax2.scatter(xi, yi, 25, zi)
ax2.set_xlim(-3, 3)
ax2.set_ylim(-3, 3)
ax2.set_title('Node selection')

ax3 = plt.subplot2grid((2,2), (1,0), projection='3d', colspan=2, rowspan=2)
#ax3.plot_surface(X, Y, Z, alpha=0.25)
#ax3.scatter(xi, yi, zi, s=25)
cset = ax3.contour(X, Y, Z, zdir='z', offset=-4)
cset = ax3.contour(X, Y, Z, zdir='x', offset=-5)
ax3.set_xlim3d(-5, 3)
ax3.set_ylim3d(-3, 5)
ax3.set_zlim3d(-4, 2)
ax3.set_title('Surface plot')
fig.tight_layout()
plt.show()

from scipy.interpolate import interp2d
interpolant = interp2d(xi, yi, zi, kind='linear')
plt.figure()
plt.axes().set_aspect('equal')
plt.pcolor(X, Y, interpolant(t, t))
plt.scatter(xi, yi, 25, zi)
CP = plt.contour(X, Y, interpolant(t, t), colors='k')
plt.clabel(CP)
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.title('Piecewise linear interpolation')
plt.show()