14 SciPy分段多项式插值

分段多项式插值(Piecewise polynomial interpolation)，顾名思义即不是用一个多项式去逼近一族点，多项式插值是用一个多项式去将一族点逼近，有的时候这唯一的多项式不能很好地将数据聚拢，预测其他点也未必准确，规避此缺点可以考虑将这一族点集合分成若干组，对每一组点集用一个多项式逼近(插值)，这样有多少组变有多少个多项式，那么整个逼近局部光滑。分段多项式逼近的每一段(每组点集)都有一个多项式，可以是一次、二次...等n次多项式，如果针对一族点集每段都是一次多项式，那么可称之分段一次多项式插值或逼近，依次类推。

14.1 SciPy分段多项式插值函数

在SciPy的0.14.0版本里提供了一个函数PiecewisePolynomial可以实现对一族点集进行分段的多项式插值实现，函数的参考文档可以访问官方网站。函数有常用的三个参数，xi、yi、和orders，xi即点集含有若干个点的x坐标的数据，yi是各阶导数值，orders的意思是各分段区间希望采用的多项式插值函数的最高幂次方，可以用列表给出各个区段上的多项式的最高次方数; 也可给出整个区间都采用某次方多项式插值多项式的最高次方数意思是都是某次多项式插值。

14.2 SciPy分段多项式插值示例

下面以 $$ f(x) = x^2 + 2x + 1 $$ 方程的曲线为例来使用一下PiecewisePolynomial函数来对这个曲线进行分段二次多项式插值测试，由于PiecewisePolynomial函数需要三个参数，那么构造如下：

xi列表在$[0,1]$上取5个点，通过numpy的linspace函数构造出来。
yi需要给出各个xi的0次和1次导数值。
由于打算做二次多项式插值，那么各段插值多项式都是二次的，故此时的order可以设置为一个纯的数2,如果打算在各个区段用不同的次方的多项式来插值，则可以用列表给出各个段上的多项式的最大值。

yi在xi上的0次导数实际就是f(x)本身，而1次导数为f'(x) = 2x + 2, 2次导数 f''(x) = 2。

编写程序如下：

#coding:utf-8
from scipy.interpolate import PPoly,interp1d,PiecewisePolynomial
import numpy as np, matplotlib.pyplot as plt

nodes = np.linspace(0, 1, 5)
x = np.linspace(0, 1, 100) 
def f(t): 
    return t**2 + 2*t + 1
print "nodes", nodes
print "f_nodes", f(nodes)
#分段一次插值
interpolant = interp1d(nodes, f(nodes), kind='linear')
plt.figure(figsize=(12,6))
plt.subplot(121, aspect='equal')
plt.plot(x, interpolant(x), 'b--', label="interpolation")
plt.plot(nodes, f(nodes), 'ro')
plt.plot(x, f(x), 'r-', label="original")
plt.legend(loc=8)
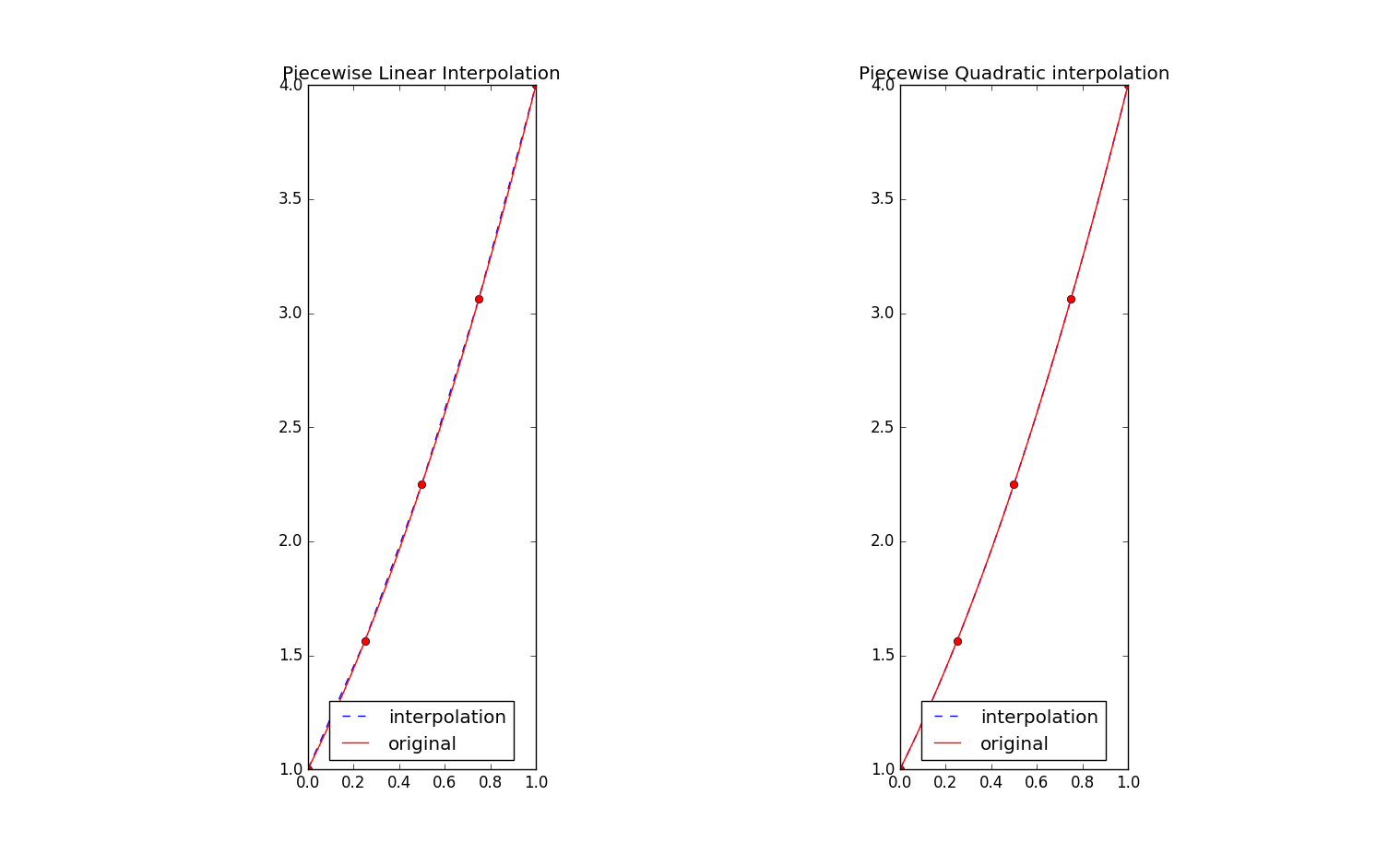
plt.title("Piecewise Linear Interpolation")

#分段二次插值
yi = np.zeros((len(nodes), 2))
yi[:,0] = f(nodes)#0次导数
yi[:,1] = 2 * nodes + 2#1次导数
print yi
#每个区段都是2次多项式插值
interpolant = PiecewisePolynomial(nodes, yi, orders=2)
print "->",interpolant(0.25)
#每个区段用不同的次的多项式插值
#interpolant = PiecewisePolynomial(nodes, yi, orders=[2,1,2,1])
print help(interpolant)
#给出
print "->",interpolant.derivatives(0.6)
plt.subplot(122, aspect='equal')
plt.plot(x, interpolant(x), 'b--', label="interpolation")
plt.plot(nodes, f(nodes), 'ro')
plt.plot(x, f(x), 'r-', label="original")
plt.legend(loc=8)
plt.title("Piecewise Quadratic interpolation")
plt.show()

程序里的print "->",interpolant(0.25)的执行结果是->1.5625怎么来的？ f(0.25) = x^2 + 2x + 1 = 0.0625 + 0.5 + 1 = 1.5625。

程序里interpolant.derivatives(0.6)的执行结果是插值函数在x = 0.6处的各阶导数值[2.56 3.2 2. ]，能和函数f(x)的各阶导数对应上么? 分析、计算如下：分别是插值函数的0次、1次和2次的导数值，由于函数f(x) = x^2 + 2x + 1的0次为f(0.6)= 0.36 + 1.2 + 1 = 2.56,一次导数为f'(0.6)= 2 x 0.6 + 2 = 3.2,二次导数f''(0.6) = 2和结果是一一对应的。程序执行的可视化输出如下所示：