5. Scipy Tutorial-无约束优化

SciPy的optimize模块提供了许多数值优化算法、函数最小值(标量或多维)、曲线拟合和寻找等式的根的有用算法。该scipy.optimize模块包含以下几个方面：

使用各种算法(例如BFGS，Nelder-Mead单纯形，牛顿共轭梯度，COBYLA或SLSQP)的无约束和约束最小化多元标量函数(minimize())
全局(蛮力)优化程序(例如，anneal()，basinhopping())
最小二乘最小化(leastsq())和曲线拟合(curve_fit())算法
标量单变量函数最小化(minim_scalar())和根查找(newton())
使用多种算法(例如，Powell，Levenberg-Marquardt混合或Newton-Krylov等大规模方法)的多元方程系统求解(root)

优化问题，指在某些约束条件下，决定某些可选择的变量应该取何值，使所选定的目标函数达到最优的问题。在数学最优化中，Rosenbrock函数是一个用来测试最优化算法性能的非凸函数，由Howard Harry Rosenbrock在1960年提出。也称为Rosenbrock山谷或Rosenbrock香蕉函数，也简称为香蕉函数。

Rosenbrock function定义如下：

$$ f(x,y)=100(y-x^2)^2+(1-x)^2 $$

它的一阶导数为：

$$ \frac {\partial }{\partial y} f (x,y) = -200{x}^{2}+200y $$

$$ \frac {\partial }{\partial x}f (x,y) =-400(-{x}^{2}+y)x-2+2x $$

当它取极值的时候它的一阶导数等于0。所以由$\frac {\partial }{\partial y} f (x,y) =0 $ 可得$y=x^2 $。代入$\frac {\partial }{\partial x} f (x,y) =0 $的式子中可解得它只有唯一解$x=1,y=1$。

Nelder-Mead Simplex algorithm (method='Nelder-Mead') 是Nelder-Mead法或称下山单纯形法，由Nelder和Mead发现（1965年），这是用于优化多维无约束问题的一种数值方法，属于更一般的搜索算法的类别。

import numpy as np
from scipy.optimize import minimize
def rosen(x):
    return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead', options={'xtol': 1e-8, 'disp': True})
print res.x

程序执行结果：

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 339
         Function evaluations: 571
[1. 1. 1. 1. 1.]

Nelder-Mead法没有使用梯度寻优，速度较慢，可以使用下面使用了梯度的bfgs法来取得最优值。

Broyden-Fletcher-Goldfarb-Shanno algorithm (method='BFGS') 多变量的Rosenbrock函数形式: $$ f(x) = \sum_{i = 1}^{N-1}(x_{i}- x_{i-1})^2 + (1 - x_{i-1})^2 \quad where\quad x = [x_1,\cdots,x_n] \in R^N $$

Rosenbrock函数的梯度向量： $$ \frac{\partial f}{\partial x_{j}} = \sum_{i=1}^{N}200(x_{i}-x_{i-1}^{2})(\delta_{i,j}-2x_{i-1}\delta_{i-1,j})-2(1-x_{i-1})\delta_{i-1,j} = 200(x_{j}-x_{j-1}^{2})-400x_{j}(x_{j+1}-x_{j}^{2})-2(1-x_{j}) $$ 特殊的j = 0和j = N - 1的梯度向量计算形式为： $$ \frac{\partial f}{\partial x_{0}} = -400x_{0}(x_{1}-x_{0}^{2})-2(1-x_{0})$$ $$\frac{\partial f}{\partial x_{N-1}} = 200(x_{N-1}-x_{N-2}^{2}) $$

import numpy as np
from scipy.optimize import minimize
def rosen_der(x):
    xm = x[1:-1]
    xm_m1 = x[:-2]
    xm_p1 = x[2:]
    der = np.zeros_like(x)
    der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)
    der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])
    der[-1] = 200*(x[-1]-x[-2]**2)
    return der
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='BFGS', jac=rosen_der, options={'disp': True})
print res.x

程序执行结果：

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 52
         Function evaluations: 64
         Gradient evaluations: 64
[1. 1. 1. 1. 1.]

对比两个程序在寻优过程中算法的迭代次数分别为339和52，显然使用了了梯度向量的BFGS速度更快！

Newton-Conjugate-Gradient algorithm - (method='Newton-CG')

$$ f(x)\approx f(x_{0})+\nabla f(x_{0})\cdot(x-x_{0})+\frac{1}{2}(x-x_{0})^{T}H(x_{0})(x-x_{0}). $$ 这里的$H(x_0)$是Hessian二阶矩阵。 $$ H_{ij}=\frac{\partial^{2}f}{\partial x_{i}\partial x_{j}} = 200(\delta_{i,j}-2x_{i-1}\delta_{i-1,j})-400x_{i}(\delta_{i+1,j}-2x_{i}\delta_{i,j})-400\delta_{i,j}(x_{i+1}-x_{i}^{2})+2\delta_{i,j} = (202+1200x_{i}^{2}-400x_{i+1})\delta_{i,j}-400x_{i}\delta_{i+1,j}-400x_{i-1}\delta_{i-1,j} $$ 若$i,j\in\left[1,N-2\right]$当$i,j\in\left[0,N-1\right])$时有：

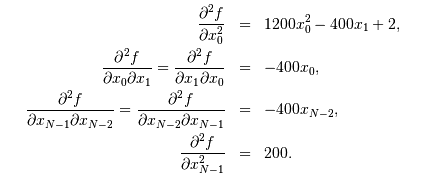假定$N=5$有：

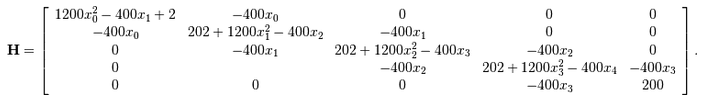
import numpy as np
from scipy.optimize import minimize
def rosen_der(x):
    xm = x[1:-1]
    xm_m1 = x[:-2]
    xm_p1 = x[2:]
    der = np.zeros_like(x)
    der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)
    der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])
    der[-1] = 200*(x[-1]-x[-2]**2)
    return der
def rosen_hess(x):
    x = np.asarray(x)
    H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)
    diagonal = np.zeros_like(x)
    diagonal[0] = 1200*x[0]**2-400*x[1]+2
    diagonal[-1] = 200
    diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]
    H = H + np.diag(diagonal)
    return H
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='Newton-CG', jac=rosen_der, hess=rosen_hess, options={'xtol': 1e-8, 'disp': True})
print res.x

程序执行结果：

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 24
         Function evaluations: 33
         Gradient evaluations: 56
         Hessian evaluations: 24
[1.         1.         1.         0.99999999 0.99999999]