8. Scipy Tutorial-极小值minimize_scalar

求单变量函数的极小值可能是最常遇见的问题，在Scipy里有个minimize_scalar函数可以快速的求得单变量的函数的机制。

• 全局极小值

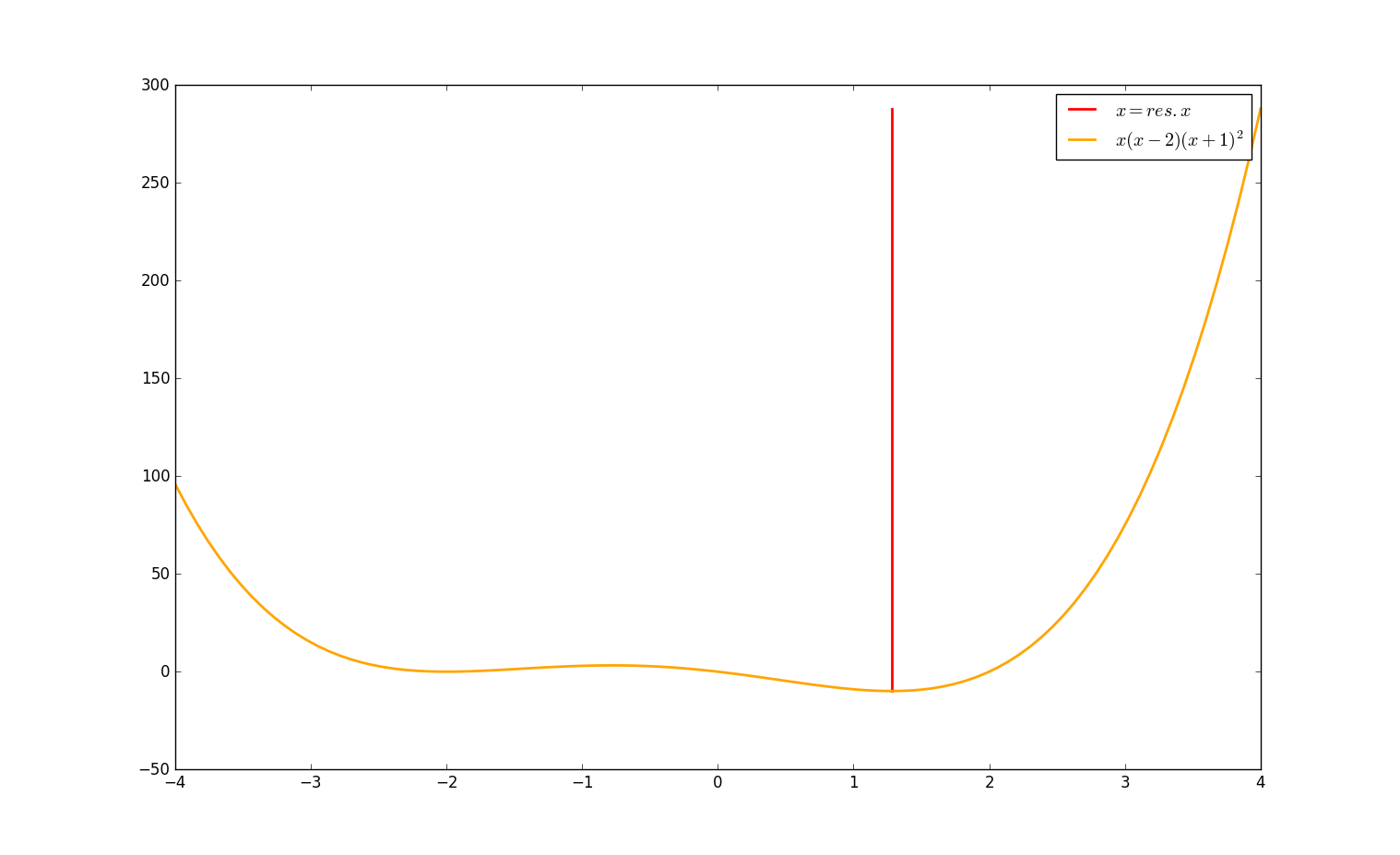
#coding:utf-8
import numpy as np
from scipy.optimize import minimize_scalar
def f(x):
    return (x - 2) * x * (x + 2)**2
res = minimize_scalar(f, method='brent')
print res.x
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
x = np.linspace(-4,4,100)
y = f(x)
t = np.linspace(f(res.x),f(4),100)
plt.plot([res.x] * len(x),t,color="red",label= "$x = res.x$",linewidth=2)
plt.plot(x,y,color="orange",label="$x(x - 2)(x + 1)^2$",linewidth=2)
plt.legend()
plt.show()

执行结果：

• 局部极小值，在minimize_scalar函数里给出一个局部区域(使用bounds 形参)，可以通过该函数求得该区域内的极小值。

#coding:utf-8
import numpy as np
from scipy.optimize import minimize_scalar
def f(x):
    return x ** 2 + 10 * np.sin(x) + 1
res = minimize_scalar(f, bounds = (-5, 0), method = 'bounded')
print "(-5, 0)", res.x
res = minimize_scalar(f, bounds = (0, 5), method = 'bounded')
print "(0, 5)", res.x
res = minimize_scalar(f, bounds = (-5, 5), method = 'bounded')
print "(-5, 5)", res.x
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
x = np.linspace(-10,10,500)
y = f(x)
plt.plot(x,y,color="orange",label="$x^2 + 10 * sin(x) + 1$",linewidth=2)
plt.legend()
plt.show()

执行结果：

(-5, 0) -1.306439349869899
(0, 5) 3.837466972104491
(-5, 5) -1.3064399324551186