12. Scipy Tutorial-一元样条插值

插值不同于拟合。插值函数经过样本点，拟合函数一般(例如:最小二乘法逼近、切比雪夫多项式、范德蒙矩阵多项式逼近)尽量靠近所有样本点穿过。常见插值方法有拉格朗日插值法、分段插值法、KroghInterpolator样条插值法、Hermite插值法等。

前边使用过线性插值linear、最邻近插值nearest以及三次插值cubic，这些插值凸点点多，不够光滑，本章研究样条插值spline,实现尽量让插值函数的曲线显得更光滑(收敛性)一些。样条插值是使用一种名为样条的特殊分段多项式进行插值的形式。由于样条插值可以使用低阶多项式样条实现较小的插值误差，这样就避免了使用高阶多项式所出现的龙格现象，所以样条插值得到了流行。

scipy.interpolate包里提供了两个函数splev和splrep共同完成(B-样条:贝兹曲线(又称贝塞尔曲线))插值，和之前一元插值一步就能完成不同，样条插值需要两步完成，第一步先用splrep计算出b样条曲线的参数tck，第二步在第一步的基础上用splev计算出各取样点的插值结果。

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import splev, splrep
def f(x):
    return x ** 2 + 10 * np.sin(x) + 1
x = np.linspace(0, 10, 20)
y = f(x)
plt.plot(x, y, '*-')
plt.show()
x2 = np.linspace(0, 10, 200)
spl = splrep(x, y, s = 0)
y2 = splev(x2, spl)
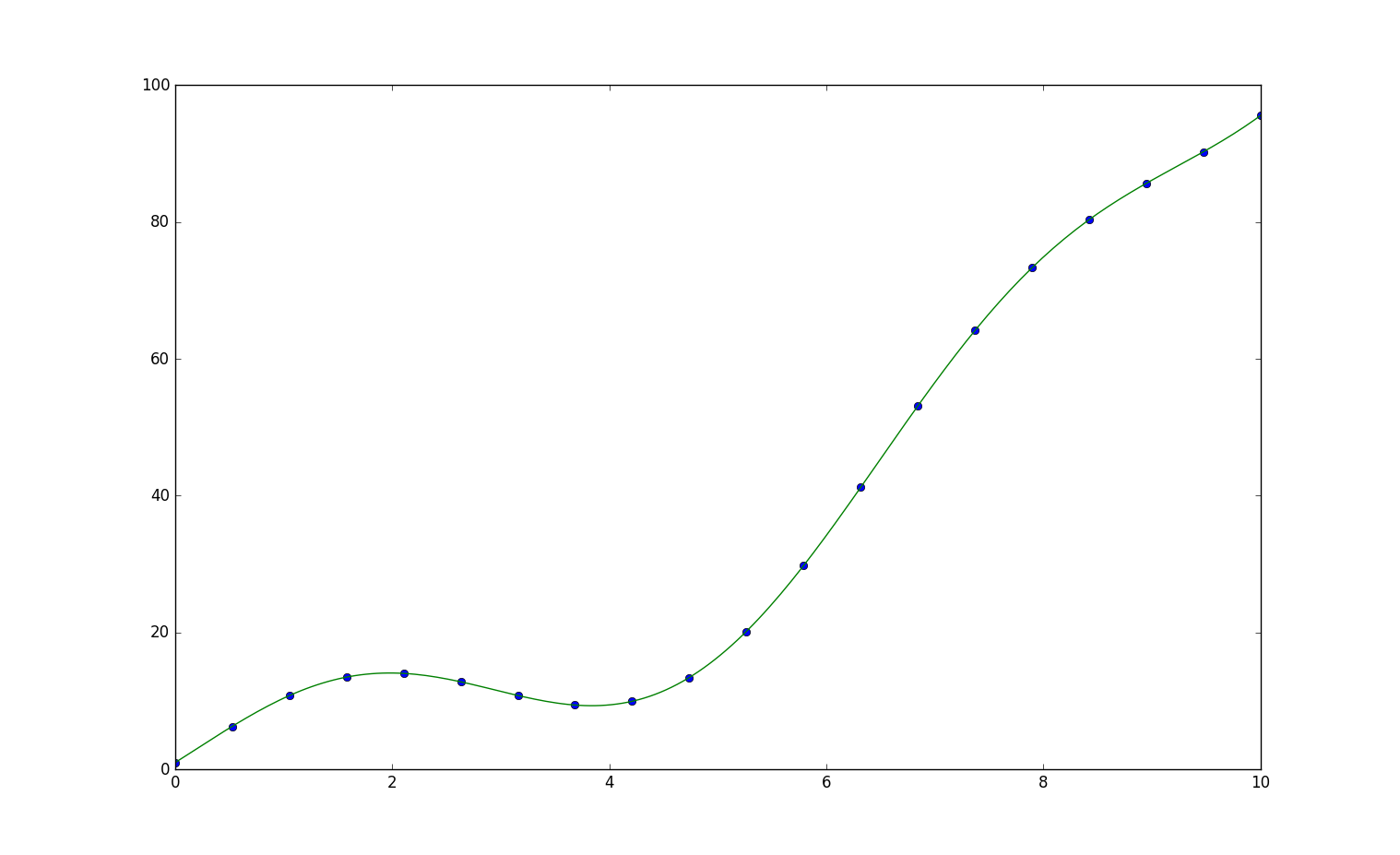
plt.plot(x, y, 'o', x2, y2)
plt.show()